Bienvenue dans la 2ième dimension
Jeunes, mes amis et moi jouions souvent avec une catégorie de jouets
nouvellement mise sur le marché de l'époque, les micromachines. Ces voitures, avions et
bateaux dont la valeur se trouvait, à nos yeux, inversement proportionnelle à leur taille,
nous les collectionnons avec un malin plaisir. À l’Université de Sherbrooke, des grands
enfants s’amusent avec des jouets vraiment plus petits que ceux offerts dans les boutiques :
les microstructures quantiques.
Construites à l’aide des techniques modernes de croissance cristalline, comme l’épitaxie par
jet moléculaire, les microstructures quantiques désignent des structures, généralement composées
de semiconducteurs, si petites que ses « habitants », les électrons, subissent des effets
quantiques. Ces éléments, en fonction du confinement imposé, se nomment puits (2D), fils
(1D) ou point (0D) quantiques. Le confinement, qui bouleverse complètement les comportements
des électrons, altère subséquemment les propriétés optique et électronique de ces structures.
Extrêmement miniaturisées, ces microstructures conçues « sur mesure » répondent à des besoins
électroniques ou optoélectroniques très précis en matière de technologie.
|
«Confiner un électron… comment vous faites ça?« Il suffit de
soumettre cet électron à des forces l’obligeant à rester en place. On peut représenter
la scène par un profil de forces où les électrons peuvent posséder des énergies plus
faibles s’ils se trouvent dans le semiconducteur B que dans le A. D’un point de vue
classique, on confine notre lapin-électron en le plaçant dans un puits dont les parois
sont trop élevées pour être escaladées. La particule quantique dans le puits possède
plusieurs états d’énergie possibles (voir Ils sont fous ces physiciens). On représente
schématiquement ces énergies par des plateaux (voir ci-contre). Pour une largeur notable
du semiconducteur B, ces plateaux sont très rapprochés. Le saut d’énergie entre ces
plateaux est, en effet, inversement proportionnel à la largeur du puits. Cependant,
la révélation quantique survient lorsque la largeur de B prend des dimensions microscopiques.
En effet, à cette échelle, les différents niveaux d’énergie deviennent perceptibles.
Dans une telle structure, le confinement ne se réalise pas systématiquement, car l’électron
se balade d’un niveau d’énergie à un autre, à son gré. En abaissant la température sous
les 1K (-272 °C), l’énergie disponible devient la plus faible possible. Alors la seule
alternative au pauvre lapin frigorifié, consiste à se placer dans le mode «économique« :
le mode de vibration du premier niveau (voir ci-contre, l’énergie E1). Telles les cordes
d’une guitare, les particules « vibrent » selon différents modes et empruntent différentes
énergies (après tout, ce sont aussi des ondes). |
D'un point de vue "classique", où le plateau de A est plus haut que B, le paresseux lapin, en B,
ne sautera pas par dessus le plateau (admettant que la température demeure basse). Qui plus est,
si la largeur 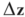 de B devient très petite, le lapin sera restreint à se déplacer selon les axes
x et y uniquement.
|
 |
 |
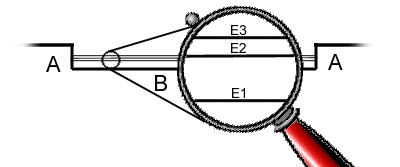
Lorsque la largeur de "B" est macroscopique |
Lorsque la largeur de "B" est microscopique |
Lors d’un confinement, l’énergie totale ne devient jamais nulle (principe d’incertitude d’Heiseinberg).
De plus, deux particules ne peuvent posséder simultanément les mêmes vitesses. Pour ces raisons et
parce que la quantification de l’énergie ne se dévoile qu’aux dimensions microscopiques, différents
phénomènes deviennent observables lors d’un confinement. L’énergie d’un tel système se définit par
la formule: E = ½ mv x2 + ½ mv y2 + e n.
On reconnaît rapidement les simples composantes du mouvement « classique », ½ mv x2
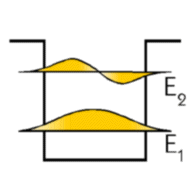
et ½ mv y2 mais où est partie la composante z? Dans la figure ci-contre, les
deux premiers modes de vibration d’un électron apparaissent « coincés » entre deux barrières de potentiel.
Sous les axes x et y (dans B), l’électron vibre à sa guise, se baladant ici et là en empruntant différentes
énergies. Toutefois, en z, le pauvre est limité à l’énergie allouée et, à basse température, seulement
à l’énergie E 1. Voilà le confinement quantique. L’électron peut vibrer de multiples façons
dans le plan x-y, mais ses choix sont réduits sous l’axe z. Connaissant l’énergie attribuée par
l’axe despotique, l’étude des phénomènes exotiques, produits lors du confinement, devient possible.
La physique fondamentale a donc quelque chose à se mettre sous la dent! Au Département de physique de
l’Université de Sherbrooke, René Côté se penche, entre autres, sur les phénomènes tels que l'effet
Hall quantique, la cristallisation des électrons (cristal de Wigner), les excitations topologiques
(skyrmions, mérons) et à certaines transitions de phase du gaz d’électrons dans les doubles puits
quantiques (des microstructures quantiques formées de deux puits quantiques séparés par une barrière
de potentiel, voir Deux puits valent mieux qu'un!).
|
|
Ça ne vous en dit pas encore assez? Laissez-moi donc vous donner une meilleure idée.
Comme cité précédemment, l’effet Hall quantique émerge, comme plusieurs autres phénomènes, du confinement
d’un gaz d’électrons. « Oui, mais c’est quoi? » L’effet Hall quantique représente, parallèlement à
l’effet Hall classique (oh! surprise!), le phénomène observé lorsqu’un puits quantique (donc 2D)
est soumis à un champ magnétique perpendiculaire (dans notre cas, dans la direction z).
Sous l’effet de celui-ci, les niveaux d’énergie électronique (les plateaux du lapin) se subdivisent
en sous niveaux d’énergie, appelés les niveaux de Landau, séparés par une énergie

où
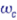
représente
la pulsation cyclotron. Chacun de ces niveaux peut « abriter » un certain nombre d’électrons, le taux de
remplissage des « appartements » Landau se note par

, où
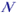
est le nombre d’électrons et

, la capacité
des niveaux (combien d’électrons peuvent habiter dans le même « bloc appartement »). En diminuant l’intensité
du champ magnétique, on s’attendrait à voir la conductivité augmenter linéairement, comme dans l’effet Hall classique,
mais le résultat n’y correspond pas exactement. Certes la conductivité croît, mais par plateaux.
Le graphe (voir ci-bas) montre la résistivité (ligne bleue) augmenter par plateaux lorsque le champ magnétique augmente.
La prévision classique est représentée en rouge.

L’ordonnée est graduée en fractions de h/e
2 . D'une manière naturelle, un multiple de la constante h/e
2
semble définir avec justesse chaque saut. Suite à cette découverte, de nouveaux étalons en matière de résistance ont été
établis d'une manière des plus précises. Attention, il ne faudrait pas confondre les fractions ci-dessus avec l’effet
Hall quantique fractionnaire, dont les auteurs se vinrent attribuer le prix Nobel de physique de 1998. Pour en savoir
plus sur l'effet Hall classique et l'effet Hall quantique fractionnaire, jetez-vous vite sur votre copie du numéro
7 de
L'Attracteur, Spécial Espace :
Le prix Nobel 1998.
Représentation de la texture magnétique d’un skyrmion. |
 |
Il est aussi intéressant d’observer les effets produits lorsque le taux de remplissage avoisine un.
Autrement dit, lorsqu'un « bloc appartement Landau » est rempli d'électrons et que le prochain « locataire »
devra « déménager » dans le « bloc 2 », lui coûtant ainsi une énergie précise. Dans la région de remplissage 1,
les électrons forment un état ferromagnétique dans lequel le sens de rotation de tous les électrons sur
eux-mêmes est identique et orienté face à la source magnétique (spin haut). En conséquence, le niveau
de Landau le plus près ou le plus proche « plateau » à escalader, pour un électron dans cette situation,
serait de se « retourner » complètement. Autrement dit, de prendre un spin « bas ». Or, il n’est pas si
simple de se retourner lorsque vous êtes un électron avec des milliers de voisins tout près de vous. En
effet, il y a une certaine interaction entre les électrons. Ainsi, en tentant de se « retourner », notre
électron met en branle tout un processus qui affecte ses proches, provoquant leur « renversement » partiel.
Un peu comme si vous dormiez sur un lit d’eau et que votre partenaire se retournerait. Ceci donne au gaz
d’électrons restreint dans deux dimensions, une texture magnétique, appelée skyrmion. Le skyrmion est un
changement « global » des spins et l'orientation des spins des électrons entourant la particule rebelle semble
former une sorte de vortex (voir image). Même formé de plusieurs particules, le skyrmion agit comme une seule
particule grâce aux propriétés quantiques de l'électron : l'électron nouvellement ajouté est maintenant « présent »
un peu partout dans le skyrmion. Ce faisant, le skyrmion interagit avec son milieu comme une particule! C’est
pourquoi il joue un rôle important dans la physique des microstructures quantiques au taux de remplissage près de
un. Ci-haut est illustré une image de topologie de spins, caractérisant le skyrmion. Pour vous donner une meilleure
perception de l’effet d’un skyrmion, regardez ci-bas, une illustration animée du phénomène.
| |
 |
Ici, chaque flèche représente le spin d'un électron. Notez le retournement individuel du spin de chaque électron, donnant
ainsi naissance à une « simili » particule. |
|
Nous pouvons finalement constater que nous sommes bien loin d’être au bout
de nos surprises et que l’univers quantique nous en réserve bien d’autres. Cependant, on ne
peut qu’admirer les progrès technologiques impliqués. En effet, dans le domaine de
l’optoélectronique, on conçoit des lasers non plus macroscopiques et ayant des fréquences
imposées par la nature des gaz, mais bien microscopiques et possédant les fréquences
précisément désirées par l’utilisateur. Non seulement stimulantes, les nouvelles découvertes
en physique des semiconducteurs assurent ainsi le développement de nos connaissances du monde
quantique promettant de futures applications littéralement surprenantes.
Tous mes remerciements au professeur René Coté qui a su investir
son précieux temps à l'élévation de ma pauvre connaissance, requise à la rédaction de cet article.
DWM
_________________________________________________






