CASSE-TÊTE
Solutions aux casse-tête du dernier numéro
- Pour un rappel de la question, cliquer ici. D’expérience, un ballon est plus difficile à gonfler au début, lorsqu’il est encore petit, et plus facile vers la fin. Cela signifie que la pression d’air à l’intérieur du ballon est plus grande quand le ballon est plus petit (c’est la pression d’air dans les poumons de celui qui gonfle un ballon qui lui cause un effort plus ou moins grand; cette pression doit être au moins aussi grande que celle à l’intérieur du ballon). Donc, dans cette situation, le ballon plus petit devrait se vider dans le plus grand lorsqu’ils sont reliés (le plus petit gonfle le plus grand)! Maintenant, pourquoi un ballon est-il plus difficile à gonfler au début? Si T(R) est la tension de la membrane en fonction du rayon et Pat la pression atmosphérique, alors la pression P du ballon est P = Pat + T(R) / R. À première vue, on pourrait croire que le matériau de la membrane obéit à la loi de Hooke, de la même manière qu’un ressort idéal produit une force proportionnelle à son élongation: T(R) = CR, où C est une constante. Si c’était le cas, la pression à l’intérieur du ballon serait indépendante du rayon du ballon ou, si on préfère, de son degré de gonflement. En réalité, le matériau polymérique de la membrane est plus difficile à étirer pour de petites élongations, c’est-à-dire que C n’est pas une constante, mais une fonction de R qui diminue avec R.
- Pour un rappel de la question
cliquer ici.
Ce phénomène d’instabilité dynamique s’explique simplement en invoquant la conservation de l’énergie et du moment cinétique d’un corps rigide. Un objet comme le livre en question possède trois axes bien déterminés avec des moments d’inertie assez différents: I1 < I2 < I3 , où I1 correspond au grand axe, I3 au petit axe et I2 à l’axe moyen. L’énergie cinétique de l’objet en rotation, en fonction des composantes de son moment cinétique par rapport à chacun de ces trois axes, est E = [(J1)2 / I1 + (J2)2 / I2 +
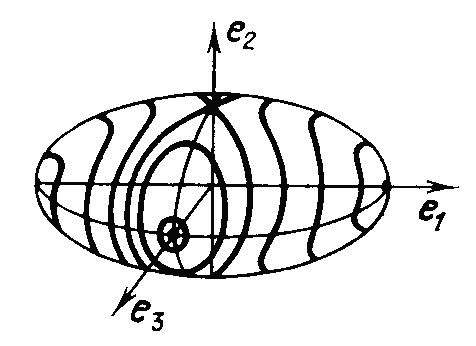
(J3)2 / I3 ] / 2 . La surface d’énergie constante est donc un ellipsoïde à trois axes assez différents. D’autre part, la conservation du moment cinétique dans un repère fixe dans l’espace signifie que, dans un repère d’axes fixés à l’objet en rotation, le vecteur moment cinétique n’est pas fixe, mais évolue sur une sphère. La conservation de l’énergie et du moment cinétique signifie donc que ce vecteur moment cinétique évolue dans le temps sur l’intersection de la sphère et de l’ellipsoïde. Or, selon le rayon de la sphère (c’est-à-dire la grandeur du moment cinétique), l’intersection entre ces deux surfaces est une courbe fermée à proximité de grand axe et à proximité du petit axe, mais est une courbe ouverte à proximité de l’axe moyen, d’où instabilité dans ce cas (voir figure).
Nouveaux casse-tête
- Prenez un verre, remplissez-le partiellement d’eau et couvrez-le d’une carte à jouer ou d’un couvercle de plat en plastique (prendre soin de prendre un diamètre plus grand que le verre pour qu’il n’y ait pas adhésion du couvercle sur les bords). Ensuite, retourner le tout à l’envers en maintenant le couvercle en place, puis lâchez ce dernier. Curieusement, le couvercle reste en place. Pourquoi? Deux phénomènes sont impliqués.
- Par une journée sans vent, le démon de la perversité vous pousse à tirer une balle de fusil exactement à la verticale et à rester sur place en attendant qu’elle retombe. Y a-t-il lieu de vous inquiéter? Où la balle retombera-t-elle, selon vous?
David Sénéchal
Dernière mise à jour: 18 novembre 1996.
Mise en page par Gilbert Vachon
 revue@physique.usherb.ca
revue@physique.usherb.ca

