Galilée marqua par ses travaux les débuts de la « vraie » physique. Sa célèbre expérience de la tour de Pise aurait démontré que, peu importe le poids des objets, ceux-ci tombent avec le même temps de chute, en négligeant, bien sûr, la résistance de l'air. Ce phénomène va à l’encontre de l’intuition, mais se vérifie par l’expérience. Ce qui amène le principe de l’inertie que raffinera Newton ultérieurement. L’inertie constitue, en quelque sorte, la résistance qu’oppose une masse à son déplacement. Avec Newton, viendront les définitions de masse inertielle et de masse dite pesante. Enfin, Galilée instaure, en quelque sorte, une première ébauche de physique « relative ». Cette relativité, fort simple de nos jours, demeure cruciale dans le développement de la physique que nous connaissons. En somme, cet homme de la Renaissance nous enseigne que l’immobilité et le mouvement uniforme ne se distinguent pas réellement l’un par rapport à l’autre. Pour illustrer ses propos, imaginez un boulet tombant du haut du mât d’un navire. Le boulet file en ligne droite et atterrit au pied du mât (à condition qu’aucun matelot ne travaille à proximité...). Cela se produit à quai ou en pleine mer pourvu que l’embarcation vogue à vitesse constante. Dans ce dernier cas, l’intuition nous indique que le boulet tombera en arrière du mât, puisque le bateau avance horizontalement durant la descente du boulet. Pourtant la réalité contredit l’intuition. Si, vue sur le bateau, la chute forme une ligne droite, du point de vue d’un observateur externe, celle-ci forme une parabole composée de la vitesse du navire et de l’accélération verticale du boulet. Ceci prouve donc que le mouvement observé dépend de la référence adoptée… Sans le vouloir, cette folle théorie insinue indirectement que la Terre ne constitue plus le centre de l’Univers, mais bien une planète, comme les six autres connues à cette période, tournant autour d’un Soleil fixe! En effet, tous les jours, nous voyons le Soleil se déplacer sur la voûte céleste. De là à proposer que la Terre tourne autour du Soleil, il n’y a qu’un pas : « Bien voyons! Et puis quoi encore? Que l’homme descend du singe? Ha! ha! ha! » Bref, une autre chicane entre la science naissante et la religion de l'époque; et ce ne serait pas la dernière...

     Newton prend la relève. Appuyé par les observations de Galilée et les idées de Descartes, Newton établit les fondements de la physique classique décrivant le mouvement. Qui ne connaît pas l’anecdote de la pomme? Selon cette légende, la chute d’une pomme au sol et le maintien de l’orbite de la Lune autour de la Terre intriguent longuement Isaac Newton. Il déduit que ces deux faits dérivent d’une même et unique force. Ce raisonnement le mène à la théorie de la gravitation universelle, selon laquelle deux corps de masse m₁ et m₂ exercent l’un sur l’autre une force d’attraction dirigée le long de la droite qui les joint, proportionnelle au produit de leurs masses et inversement proportionnelle au carré de la distance qui les sépare :

     Universelle, car cette relation s’applique à tous les corps, tant terrestres que célestes. Enfin la barrière tombe, car les mêmes lois régissent les deux « mon.des ». Par la suite, il prouve les lois tirées de l'ouvrage de Kepler sur l’astronomie. Pour y arriver, il développe, parallèlement à Leibniz, le calcul infinitésimal (léger détail…) qui deviendra l’un des fondements de la science moderne. L’action à distance, qu’insinue le formalisme de Newton, introduit la notion d'action instantanée, rejetée par les Cartésiens, qui la trouvent trop peu «mécanique». Quoi qu’il en soit, Newton a dit «hypotheses non fingo» (je ne feins pas d’hypothèse) à propos de la nature profonde de la gravité, se contentant d'expliquer les manifestations de celle-ci. Ça fonctionne, c’est l’essentiel…

     Plus tard, James Clerk Maxwell et ses amis développent, dans les années 1860, LA théorie de l’électromagnétisme, stipulant qu’électricité et magnétisme forment un phénomène de même nature. Puisque la lumière semble un phénomène électromagnétique, il unifie donc optique, électronique et magnétique! Dorénavant, ces deux théories maîtresses, celle de Galilée-Newton et celle de Maxwell, règnent de manière quasi parfaite sur le monde scientifique. Je dis bien « quasi parfaite », car il y a un accroc. En effet, il paraît que ces deux théories se contredisent! L’une stipule que toutes les vitesses sont relatives tandis que pour l’autre, les ondes électromagnétiques (lumière, rayon X, gamma, radio, etc.) voyagent à une vitesse constante, bien déterminée, ne variant pas selon le mouvement relatif de l’observateur… Une situation bien embarrassante pour les deux clans.

     Tenez bon! Einstein, à la rescousse, propose une solution efficace, mais peu commune! Le petit employé du Bureau des brevets, en Suisse, propose de réunir les deux grandes théories. Cependant, il faudra faire quelques petites concessions, comme remettre en question le caractère absolu du temps! Les observations démontrent que la vitesse de la lumière demeure invariable. Par exemple, si vous marchez à 1 m/s dans un train roulant à 30 m/s (environ 100 Km/h), un observateur externe au wagon vous verra avancer à 31 m/s. Or, si vous projetez un faisceau de lumière dans ce même wagon à une vitesse de 300 000 000 m/s (approximativement), l’observateur externe ne voit as le faisceau de lumière se propager à 300 000 030 m/s, bien à 300 000 000 m/s aussi! Ceci ne cadre pas avec la physique classique de Galilée-Newton. Einstein stipule que si la vitesse de la lumière demeure constante pour tous les référentiels, alors le temps lui se relativise! Ainsi, deux événements apparaîtront simultanés pour un observateur, mais pas pour un autre. Ne concernant que les observateurs en mouvement rectiligne uniforme, la théorie de la relativité restreinte joint ainsi espace et temps. L’univers tridimensionnel classique cède la place aux quatre variables de longueur, hauteur, profondeur et temps : les quatre dimensions. Ainsi, lorsque approchant la vitesse luminique, l’espace entourant une particule se contracte et le temps se dilate par rapport à un observateur. Découlent des équations d’Einstein : la limite absolue des vitesses, celle de la lumière, et sa célèbre formule E = mc² qui met en place l’équivalence de la matière et de l’énergie par le biais de l’ultime vitesse c.

     « Bon d’accord c’est bien chouette tout ça, mais où est le lien avec la gravité? » Patience, il faudra attendre quelques années plus tard, en 1915, l’arrivée de la relativité générale. Einstein, à la manière des Cartésiens de l’époque de Newton, remet en question le caractère instantané de la propagation de la gravité. Sa récente théorie limite à la vitesse c toute influence se propageant dans l’univers. Alors soit il s’est trompé, soit la théorie de Newton ne représente qu’une approximation, car la gravité n’agit pas instantanément. Un peu comme la pomme de Newton, une « illumination » éclaira un jour Einstein. Imaginez-vous dans un ascenseur en chute libre (accélération constante). Si vous y lâchez une pomme, elle « flottera » dans les airs puisqu’elle tombe de la même manière que le système, comme en apesanteur (voir l’image ci-haut). Einstein en conclut qu’accélération et gravité ne peuvent se distinguer. Les forces d’inertie ne se différencient pas. Oubliez la source même de la « gravitation » (que ce soit la Terre ou une accélération vers le haut de 9.80 m/s², personne n’y verra jamais de différence) et concentrez-vous sur l’effet de cette gravitation, quelle soit matérielle ou cinématique on s’en fiche, c’est la même chose! (E = mc²). 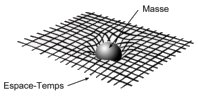Alors survient le postulat d’Einstein : l’effet de la gravité provient d’une déformation de l’espace-temps! 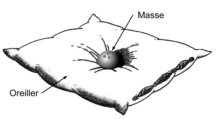La gravité n’apparaît plus comme une force, proprement dite, mais comme une courbure des quatre dimensions engendrée par la matière (ou l’énergie). Pour illustrer cet effet, imaginez une boule de quille sur un oreiller. Le creux produit représente la déformation de l’espace-temps par un astre. Lancez une petite bille sur l’oreiller et vous verrez celle-ci tendre vers la boule de quille, à moins que vous ne lui donniez une certaine vitesse tangentielle, alors la bille entrera en « orbite » autour de la sphère massive. Un peu comme la bille « Terre » fait autour de la boule « Soleil ».