« Dans le coin droit, arborant
le maillot bleu et faisant 153 kilos à la pesée :
la théorie générale de la relativité! Du coté opposé, vêtue de rouge et faisant
aussi 153 kilos à la pesée : la théorie quantique! Mesdames et messieurs, faites
vos jeux! » Oui, faites vos jeux… Pour qui allez-vous parier?
Il faut bien prendre parti puisque les deux titans
de la physique demeurent, depuis leur création, incompatibles : l’une ne peut tenir
compte de l’autre sans aboutir à certaines aberrations. Pour l’instant, on se
complaît à parier sur les deux en même temps, utilisant tantôt l’une ou parfois
l’autre pour expliquer différents phénomènes… Et encore, maintes interrogations
demeurent insolvables par les deux colosses : « D’où proviennent les quatre forces
rencontrées? Pourquoi observons-nous autant de types de particules élémentaires?
Pourquoi les particules possèdent-elles des masses, des charges ou des spins?
Pourquoi l’Univers semble-t-il quadridimensionnel? De quelle nature est l’espace-temps?
etc. » Bref, les questions ne manquent pas, mais l’outillage disponible, lui, semble insuffisant.
Depuis une trentaine d’années, un arbitre tente de
s’interposer : la théorie des cordes. Cette théorie vient mettre un terme
aux cauchemars des physiciens en essayant de combiner théorie quantique et
gravité. Comment compte-elle s’y prendre? Avec des bouts de ficelles bien
spéciales. Imaginez une corde de guitare qu’on fait vibrer en la pinçant.
Le son qu’elle produit est un mélange de plusieurs harmoniques, c’est-à-dire de
plusieurs modes d’oscillation. Selon la théorie des cordes, notre univers
serait basé sur de minuscules cordes vibrant à différents modes d’excitations.
Ces différents modes seraient les particules élémentaires observées en laboratoire.
Même si elles ne sont pas reliées à une guitare, ces cordes possèdent
tout de même une tension, inversement proportionnelle au carré de leur
longueur. Si la théorie des cordes se veut une théorie de la gravité
quantique, la longueur de ces ficelles devra être de l’ordre de la
longueur de Planck. Cette longueur est l’échelle où l’on prédit une
gravité quantique et s’avère de l’ordre de 10-35m… Oui, c’est petit.
D’accord c’est VRAIMENT très très petit! Non, un millionième d’un
milliardième de milliardième de milliardième de centimètre n’est certes
pas chose facilement observable. De plus, un autre léger détail
bloque la ruée vers les supercordes : l’énergie. Actuellement,
pour « observer » des phénomènes à très petite échelle, les
physiciens bombardent généralement une particule avec
d’autres particules. Un accélérateur de particules est
comme un microscope utilisant une longueur d’onde l =
h/p, où h est la constante de Planck et p la quantité de mouvement
de la particule accélérée. Pour observer de très petits objets,
il faut une longueur d’onde au moins aussi petite et par conséquent
des particules de très grande quantité de mouvement, donc de très
grande énergie. D’ici quelques années, les accélérateurs de particules
les plus modernes fourniront probablement une énergie du domaine de
104 GeV. Or, afin d’éventuellement observer l’effet des
cordes, donc des distances de 10-35 m, on estime qu’il
faudrait balancer une énergie dépassant les 1019 GeV,
l'énergie de Planck : plus d’un million de milliards de fois que ce
qu’on croit pouvoir se permettre d’ici dix ans! Voilà pourquoi les
physiciens opérant dans cette branche ont intérêt trouver un autre
moyen pour prouver la théorie des cordes.
|
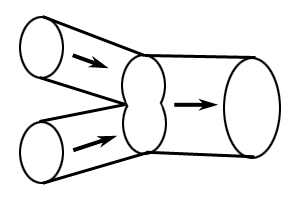
Cette paire de pantalons infiniment
petite, démontre comment les cordes pourraient se lier pour former une autre corde aux
propriétés différentes. La réaction contraire est aussi possible. |
|
Le plus étrange avec cette théorie provient de sa subdivision en six.
Aussi curieux que cela puisse paraître, la théorie de « l’unification »
approche le problème à différents angles à la fois… Étudierons-nous
seulement des cordes fermées ou ouvertes? Ensuite, nous penchons-nous
sur les fermions seulement ou sur les bosons aussi? Ces questions donnent
naissance aux différentes branches de la théorie mère. Par exemple, afin
d’inclure les fermions à la théorie, celle-ci nous oblige à amener le
concept de supersymétrie. Cette même symétrie insinue qu’à chaque boson
correspond un fermion de même masse. Sommairement, la supersymétrie relie
les particules transmettant les forces à celles constituant la matière.
Une explication du fait qu’aucun partenaire « supersymétrique » n’a jamais
été observé veut que cette absence soit due à la masse trop imposante de
ces particules, ainsi indécelables dans les accélérateurs actuels. On
estime que d’ici 2005, les accélérateurs de particules deviendront
assez puissants pour observer ces petits timides. Voilà au moins un
espoir pour les fervents de la dite théorie !
Oh! J’oubliais presque de faire mention
d’une des facettes la plus « amusante », mais non moins sensée,
du nouveau médiateur : ses dimensions. Pour que la mathématique
de la théorie des cordes, étudiant les bosons, soit cohérente,
elle requiert non pas 4, mais 26 dimensions! Dans les cinq
autres théories des cordes, exemptées de bosons, on réussit
à diminuer ce nombre à 10… Cependant, l’idée n’est pas
nouvelle. En effet, celle-ci germa dans l’esprit de Kaluza
et Klein dès les années 1920. Ceux-ci démontrèrent que
de très petites dimensions, enroulées sur elles-mêmes
à la manière de tores, pourraient très bien coexister
avec les quatre dimensions que nous connaissons, n’altérant
nullement les propriétés relativistes de l’espace et du temps
émis par Einstein quelques années auparavant.

À la manière de tores, il serait
possible pour de petites dimensions spatiales, de s'enrouler
sur elles-mêmes. Ce serait en raison de leur infime longueur
(10-35 m) qu'on ne pourrait les détecter.
|
Pour conclure, il ne suffirait plus qu’à regrouper toutes ces
différentes théories en une seule et même théorie (n’était-ce
pas là l’objectif de départ?). Une fois que la « M theory »,
ou mère de toutes les théories, sera constituée, il ne resterait
qu’à prouver le tout expérimentalement! Certes, la théorie
des cordes a, depuis trente ans, apporté très peu d'éléments
nouveaux, considérant les ressources déployées en son sens.
Il faut bien avouer que le défi à relever est de taille, que
les conséquences imposées paraissent difficilement observables
et que les mathématiques impliquées demeurent franchement
complexes. Espérons seulement que les théoriciens s’y
affairant ne perdront pas trop rapidement patience…
|
DWM
_________________________________________________

