Solutions aux casse-tête du dernier numéro

Question 1

1. Il suffit de mettre en rotation chacune des deux sphères sur une surface, à la manière d'une toupie, et ensuite de les immobiliser subitement et brièvement et de les relâcher immédiatement. La sphère pleine va demeurer immobile, alors que la sphère creuse va reprendre partiellement son mouvement de rotation, en raison du fluide à l'intérieur qui a continué de tourner lors de l'immobilisation et qui communique graduellement son mouvement à la partie rigide de la sphère. C'est ainsi qu'on distingue un oeuf dur d'un oeuf cru. On pourrait mesurer le rayon de la cavité remplie de mercure en utilisant la sphère comme pendule, en la suspendant par une corde légère et assez courte et en mesurant la fréquence des petites oscillations. Cette fréquence, pour un objet rigide, est donnée par [mgl/(I+ml²)]^1/2 , où l est la distance entre le pivot du pendule et le centre de la sphère, et I est le moment d'inertie de la sphère par rapport à son centre. La sphère creuse serait différente en ce que seule sa partie rigide contribuerait au moment d'inertie, et donc I serait plus petit dans ce cas, et donc la fréquence d'oscillation serait plus grande. En mesurant cette fréquence, on peut donc mesurer I et, par conséquent, le rayon de la partie creuse de la sphère.

Question 2

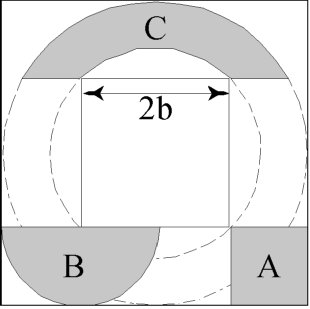2. Ce problème est difficile. Considérons la figure, où on suppose que le corridor a une largeur unité. Pour fins d'arguments, on a illustré un corridor refermé sur lui-même en carré, comme dans un édifice de même forme. À première vue, le plus gros objet qu'on pourrait glisser sur le coin du corridor est un carré de largeur unité (A). On voit cependant qu'on peut faire mieux avec un demi-cercle (B), de surface p/2 = 1,570796... Il suffit de le tourner une fois arrivé au bout du corridor. Mais on peut faire encore mieux avec un anneau (C), dont le rayon extérieur est b+1 et le rayon intérieur bÖ2, coupé de telle manière à s'insérer dans la portion droite du corridor. L'aire de cette portion d'anneau dépend de b, et vaut p/2 quand b=0 (cas de l'objet B) et zéro quand b=1/(Ö2-1)=2,4142... Il se trouve que l'aire, dans ce cas, admet un maximum de 1,9489896... quand b=0,700196... C'est là la meilleure solution que j'ai pu trouver, mais je n'ai pas de preuve que c'est la meilleure...