Casse-tête

Solutions du casse-tête du dernier numéro

1. Soit V, le potentiel électrique à l'un des sommets du cube et V₀, le potentiel au centre du cube. Comme le côté L du cube est la seule longueur disponible dans le problème, V peut être exprimé comme V = CQ/L, où Q est la charge totale contenue dans le cube et C, une constante qui ne dépend ni de la charge, ni des dimensions du cube, mais seulement de sa forme. De même, on peut écrire V₀ = C₀Q/L, où C₀ est une constante différente. Maintenant, divisons le cube en huit cubes identiques de côté L/2 et de charge Q/8. Le potentiel au sommet d'un des petits cubes est C (Q/8)/(L/2). Le centre du gros cube coïncide alors avec les sommets des huit petits cubes. Par le principe de superposition, le potentiel V₀ = C₀Q/L au centre du gros cube est la somme des potentiels aux sommets des huit petits cubes, à savoir 8C (Q/8)/(L/2) = 2CQ/L = 2V. Donc, V₀ = 2V : le potentiel au centre du cube est deux fois plus élevé qu'à son sommet. Notons qu'on ne peut utiliser le principe de superposition dans ce cas que si le potentiel est nul à l'infini, afin qu'il reste nul à l'infini même après superposition.

2. Il est hors de question d'utiliser les lois de Kirchhoff pour résoudre ce problème. Utilisons plutôt le principe de superposition. Considérons un courant I injecté au point A et s'écoulant vers les bords (lointains) de la grille. Chacune des résistances reliées au point A porte une part égale de ce courant, soit I/4. Considérons ensuite la situation inverse, où un courant I est retiré du point B (voisin de A). Dans ce cas, chacune des 4 résistances reliées à B porte un courant I/4 vers B, en provenance des bords de la grille. Superposons maintenant ces deux situations. Plus aucun courant ne parvient aux bords de la grille : tout ce qui est injecté en A est retiré en B. La chute de tension en A et B est RI/2, car I/2 est le courant net porté par la résistance reliant directement A et B. Donc la résistance équivalente entre A et B est R/2.

Nouveaux casse-tête

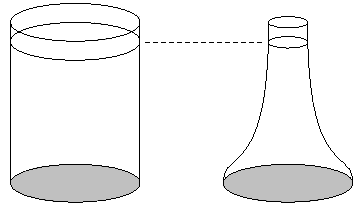1. Les deux récipients de la figure ont des fonds de même surface alors que celui de droite a un col beaucoup plus étroit. Ils sont tous les deux remplis d'eau au même niveau, celui de droite contenant bien sûr beaucoup moins d'eau que celui de gauche. La force que l'eau exerce sur le fond du récipient de gauche est-elle la même que celle exercée sur le fond du récipient de droite? Ce problème a été résolu la première fois par Simon Stevin au XVI^e siècle.

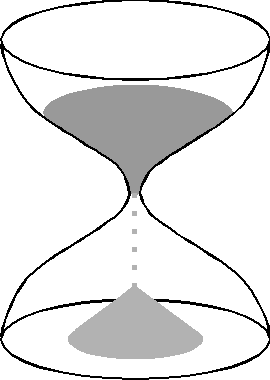2. On pose un sablier sur une balance très précise. Y a-t-il une variation du poids du sablier (tel mesuré par la balance) entre le début et la fin de l'écoulement du sable de la partie supérieure vers la partie inférieure?

a David Sénéchal